Single-source Shortest Path (Unweighted)

If a graph has unweighted edges, then finding the shortest path from one vertex to another is the same as finding the path with the fewest hops. Think of Six Degrees of Separation and Friend of a Friend. Unweighted Shortest Path answers the question "How are you two related?" The two entities do not have to be persons. Shortest Path is useful in a host of applications, from estimating influences or knowledge transfer, to criminal investigation.

When the graph is unweighted, we can use a "greedy" approach to find the shortest path. In computer science, a greedy algorithm makes intermediate choices based on the data being considered at the moment, and then does not revisit those choices later on. In this case, once the algorithm finds any path to a vertex T, it is certain that that is a shortest path.

This algorithm finds an unweighted shortest path from one source vertex to each possible destination vertex in the graph. That is, it finds n paths.

If your graph has weighted edges, see the next algorithm. With weighted edges, it is necessary to search the whole graph, whether you want the path for just one destination or for all destinations.

Specifications

CREATE QUERY tg_shortest_ss_no_wt (VERTEX source, SET<STRING> v_type,
  SET<STRING> e_type, INT output_limit = -1, BOOL print_accum =TRUE,
  STRING result_attr ="", STRING file_path ="", BOOL display_edges =FALSE)

Characteristic Value

Characteristic	Value
Result	Computes a shortest distance (INT) and shortest path (STRING) from vertex source to each other vertex.
Input Parameters	`VERTEX source`: ID of the source vertex `SET<STRING> v_type`: Names of vertex types to use `SET<STRING> e_type`: Names of edge types to use `INT output_limit`: If >=0, max number of vertices to output to JSON. `BOOL print_accum`: If True, output JSON to standard output `STRING result_attr`: If not empty, store distance values (INT) to this attribute `STRING file_path`: If not empty, write output to this file. `BOOL display_edges`: If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.
Result Size	V = number of vertices
Time Complexity	O(E), E = number of edges
Graph Types	Directed or Undirected edges, Unweighted edges

Result

Computes a shortest distance (INT) and shortest path (STRING) from vertex source to each other vertex.

Input Parameters

VERTEX source: ID of the source vertex
SET<STRING> v_type: Names of vertex types to use
SET<STRING> e_type: Names of edge types to use
INT output_limit: If >=0, max number of vertices to output to JSON.
BOOL print_accum: If True, output JSON to standard output
STRING result_attr: If not empty, store distance values (INT) to this attribute
STRING file_path: If not empty, write output to this file.
BOOL display_edges: If true, include the graph’s edges in the JSON output,

so that the full graph can be displayed.

Result Size

V = number of vertices

Time Complexity

O(E), E = number of edges

Graph Types

Directed or Undirected edges, Unweighted edges

Example

In the below graph, we do not consider the weight on edges. Using vertex A as the source vertex, the algorithm discovers that the shortest path from A to B is A-B, and the shortest path from A to C is A-D-C, etc.

[
  {
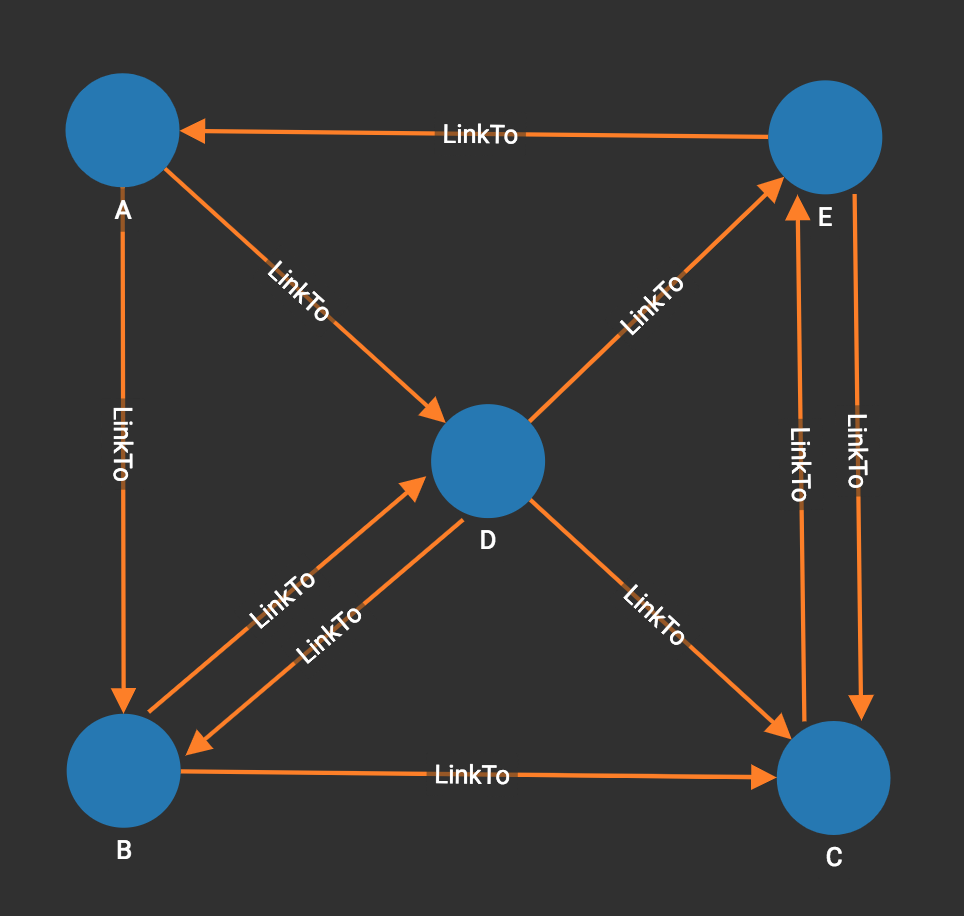
    "ResultSet": [
      {
        "v_id": "B",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 1,
          "ResultSet.@path": [
            "A",
            "B"
          ]
        }
      },
      {
        "v_id": "A",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 0,
          "ResultSet.@path": [
            "A"
          ]
        }
      },
      {
        "v_id": "C",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 2,
          "ResultSet.@path": [
            "A",
            "D",
            "C"
          ]
        }
      },
      {
        "v_id": "E",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 2,
          "ResultSet.@path": [
            "A",
            "D",
            "E"
          ]
        }
      },
      {
        "v_id": "D",
        "v_type": "Node",
        "attributes": {
          "ResultSet.@dis": 1,
          "ResultSet.@path": [
            "A",
            "D"
          ]
        }
      }
    ]
  }
]