Betweenness Centrality

The Betweenness Centrality of a vertex is defined as the number of shortest paths that pass through this vertex, divided by the total number of shortest paths. That is

\[BC(v) =\sum_{s \ne v \ne t}PD_{st}(v)= \sum_{s \ne v \ne t} SP_{st}(v)/SP_{st} ,\]

where \(PD\)is called the pair dependency, \(SP_{st}\)is the total number of shortest paths from node s to node t and \(SP_{st}(v)\)is the number of those paths that pass through v.

The TigerGraph implementation is based on A Faster Algorithm for Betweenness Centrality by Ulrik Brandes, Journal of Mathematical Sociology 25(2):163-177, (2001). For every vertex s in the graph, the pair dependency starting from vertex s to all other vertices t via all other vertices v is computed first,

\(PD_{s*}(v) = \sum_{t:s \in V} PD_{st}(v)\).

Then betweenness centrality is computed as

\(BC(v) =\sum_{s:s \in V}PD_{s*}(v)/2\).

According to Brandes, the accumulated pair dependency can be calculated as

\[PD_{s*}(v) =\sum_{w:v \in P_s(w)} SP_{sv}(v)/SP_{sw} \cdot (1+PD_{s*}(w)) ,\]

where\(P_s(w)\), the set of predecessors of vertex w on shortest paths from s, is defined as

\[P_s(w) = \{u \in V: \{u, w\} \in E, dist(s,w) = dist(s,u)+dist(u,w) \} .\]

For every vertex, the algorithm works in two phases. The first phase calculates the number of shortest paths passing through each vertex. Then starting from the vertex on the most outside layer in a non-incremental order with pair dependency initial value of 0, traverse back to the starting vertex

This algorithm query employs a subquery called bc_subquery. Both queries are needed to run the algorithm.

Specifications

CREATE QUERY tg_betweenness_cent(SET<STRING> v_type, SET<STRING> e_type,
STRING re_type,INT max_hops=10, INT top_k=100, BOOL print_accum = True,
STRING result_attr = "", STRING file_path = "", BOOL display_edges = FALSE)

Parameters

Characteristic Value

Result

Computes a Betweenness Centrality value (FLOAT type) for each vertex.

Required Input Parameters

  • SET<STRING> v_type: Names of vertex types to use

  • SET<STRING> e_type: Names of edge types to use

  • +SET<STRING> re_type: +Names of reverse edge types to use

  • INT max_hops: If >=0, look only this far from each vertex

  • INT top_k: Sort the scores highest first and output only this many scores

  • BOOL print_accum: If True, output JSON to standard output

  • STRING result_attr: If not empty, store centrality values (FLOAT) to this attribute

  • STRING file_path: If not empty, write output to this file.

  • BOOL display_edges: If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.

Result Size

V = number of vertices

Time Complexity

O(E*V), E = number of edges, V = number of vertices.

Considering the high time cost of running this algorithm on a big graph, the users can set a maximum number of iterations. Parallel processing reduces the time needed for computation.

Graph Types

Undirected edges, Unweighted edges

Example

In the example below, Claire is in the very center of the graph and has the highest betweenness centrality. Six shortest paths pass through Sam (i.e. paths from Victor to all other 6 people except for Sam and Victor), so the score of Sam is 6. David also has a score of 6, since Brian has 6 paths to other people that pass through David.

# Use _ for default values
RUN QUERY tg_betweenness_cent(["Person"], ["Friend"], _, _, _, _, _, _)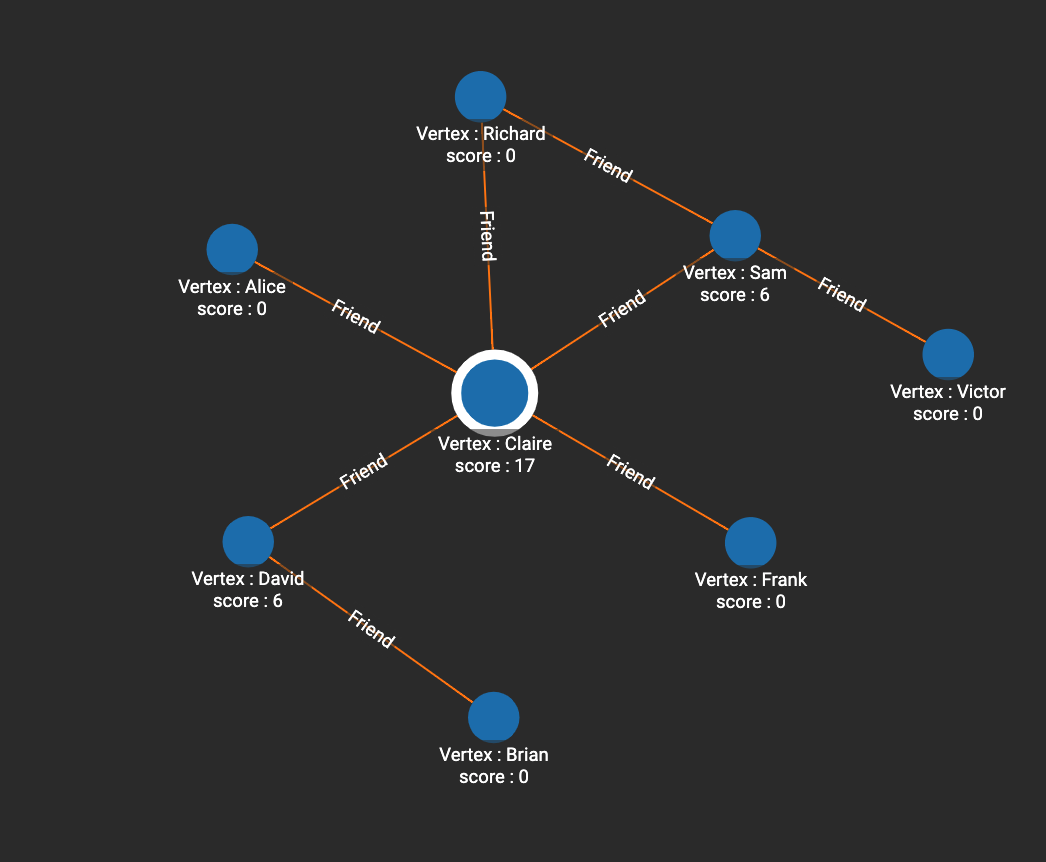
Visualized results of example query on a social graph with undirected edges Friend 
[
  {
    "@@BC": {
      "Alice": 0,
      "Frank": 0,
      "Claire": 17,
      "Sam": 6,
      "Brian": 0,
      "David": 6,
      "Richard": 0,
      "Victor": 0
    }
  }
]

In the following example, both Charles and David have 9 shortest paths passing through them. Ellen is in a similar position as Charles, but her centrality is weakened due to the path between Frank and Jack.

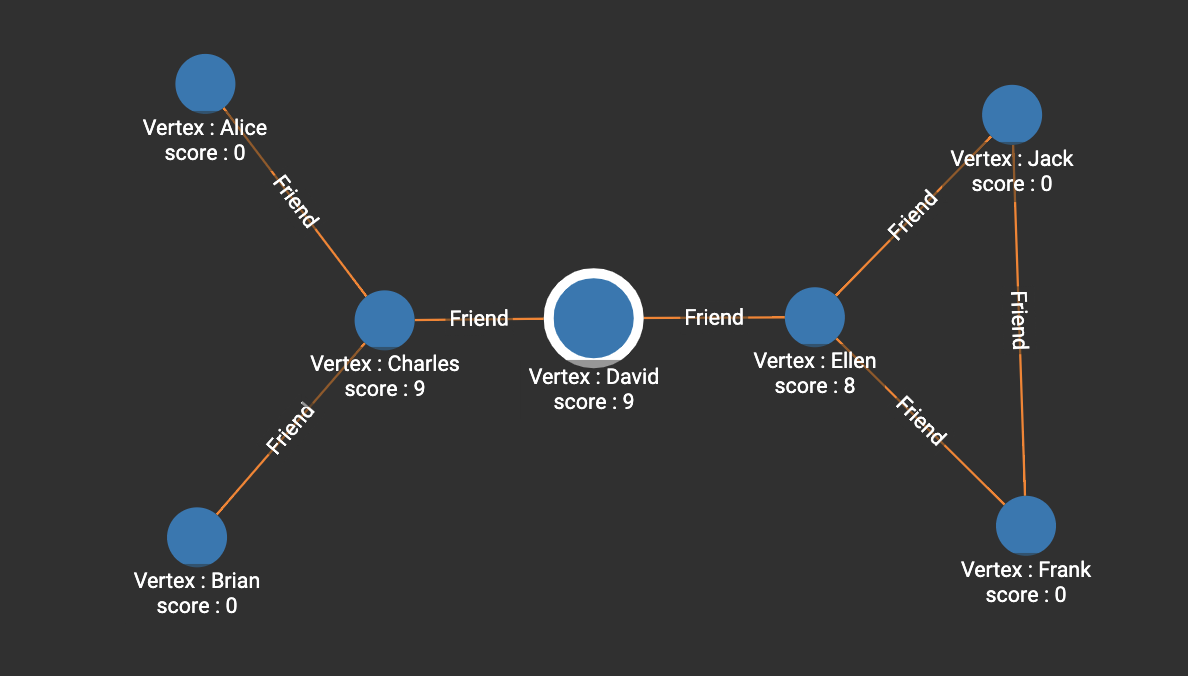
Visualized results of example query on a social graph with undirected edges Friend 
[
  {
    "@@BC": {
      "Alice": 0,
      "Frank": 0,
      "Charles": 9,
      "Ellen": 8,
      "Brian": 0,
      "David": 9,
      "Jack": 0
    }
  }
]